Sift尺度不变特征变换匹配算法 Scale Invariant Feature Transform 主要的思路就是使用高斯金字塔和高斯核滤波查分来提取局部特征。在尺度空间当中寻找极值点,提取位置、尺度和旋转不变量。
Sigema代表高斯分布的方差,尺度空间可以定义为原始图像I(x,y)与一个可变吃段高斯函数G(x,y,sigema), 。 Sigema,sigema是高斯金字塔的尺度参数,sigema越小,图像被平滑越小,相应的尺度就越小。当sigema连续变化,G(x,y,z)就生成了图像的尺度空间。 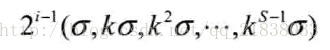 先介绍一下尺度空间理论: 用来模拟图像数据的多尺度特征,高斯卷积核是实现初读变化的唯一线性核:高斯金字塔就是为了得到不同空间下的稳定关键点,将图像和不同的尺度因子的高斯核进行卷积操作, 假设有o组,每一个组都有s层,通过一定的知识,可以的得到,组内尺度和组件尺度归结为:
第一步 将原图分离模糊成告诉金字塔模型,实际上就是使用高斯模糊将特征提取出来,
模板大小为m*n的模板元素(x,y),对整个图像进行滑移,在滑移之前,要注意边界的影响。 Sigema取值的不同,会导致不同的边缘处理效果。 使用不同的系数k的sigema,会生成一系列高斯特征:
如上图所示,想生成一阶的图,同一阶的图的sigema相同,但是k不同,然后使用个点取样的方法,生成第二阶的图形,继续使用不同倍数的sigema来对图形进行遍历,得到第二阶高斯图。为了有效的在尺度空间当中检测到关键点,定义图像的高斯差分尺度空间为图像对的不同吃多那个空间的差,可以利用dog高斯查分算子生成。 每一组高斯图,都会生成s-1个高斯差。随着高斯空间尺度的逐渐增大,对图像的模糊逐渐增大。 关键点是有dog空间的局部极值点组成的。 极值点的寻找方法就是: Dog尺度空间中的中间曾的每一个下像素和它同尺度的8个相邻点以及上下相邻尺度对应的9*2个点,以确保在尺度空间和二位图像空间当中都能检测到局部极值点。 下一步的工作就是通过进一步的检验来定位精确的关键点。具体来说就是去除噪声和边缘相应。 关键点方向的分配: 通过尺度不变性求关键点,可以使其具有缩放不变的性质每一组都有隔点采样。这一点可以取得。利用关键点领域像素的梯度方向分布特性,就可以使得图像具有旋转不变性。 在这里使用的是一阶微分模板来进行的。 然后使用1.5sigema的半圆统计进行直方图的绘制。这个直方图就是 特征点描述点的生成: 特征描述子的生成的大致思路是: 在特征点附近生成块,计算分块的梯度,生成独特的信息标记
第一步:确定描述子所需要的区域,考虑到一些因素,区域为3(d+1),原型区域的半径为3(d+1)*根号2 = R. 2:考虑到旋转不变性,将R*R领域的坐标旋转Θ,● 3:前两步是确定块的大小,到了这一步就是将关键点确定为R园的中心点,计算幅值和角度。
